(Spoilers for Star Trek: Discovery Episodes 1 and 2. Be sure to check out our summary analysis of the series premiere if you haven’t already.)
Put yourself in the captain’s chair of the USS Shenzhou. You’re in Federation territory, facing off against a Klingon warship. Its intentions are unknown. Do you maintain a defensive posture, or do you attack without provocation?
Star Trek: Discovery’s two leads disagree on a course of action, and this moment of tension between them is perhaps the best scene in the series’ promising debut. It’s also a great illustration of the Prisoner’s Dilemma. That’s right folks, it’s time for some game theory.
“They don’t appear to pose an imminent threat.”

Georgiou and lens flare, at Tanagra.
For those of you who haven’t graduated from Starfleet Academy, attended business school, or been subject to an insufferable rant about it on the internet, the Prisoner’s Dilemma is a Game Theory thought experiment that helps model decision making and trade-offs. (If you need more of an explainer than this, I refer you to one of several past articles we’ve written that use this analytical framework.) In the scenario from Star Trek: Discovery, the Klingons and the Federation both can choose to maintain a defensive posture or go on the attack.
Captain Georgiou plays by the Federation book: she thinks the Klingons don’t pose an imminent threat, but more importantly to her, she’s acting as the guardian of the Federation’s moral authority as a non-aggressive, peace-promoting organization. Its whole model of governance depends on not being seen as violent overlords who would blow their rivals away without provocation. Regardless of of the Klingon’s intentions, she sees defense as the only viable option.
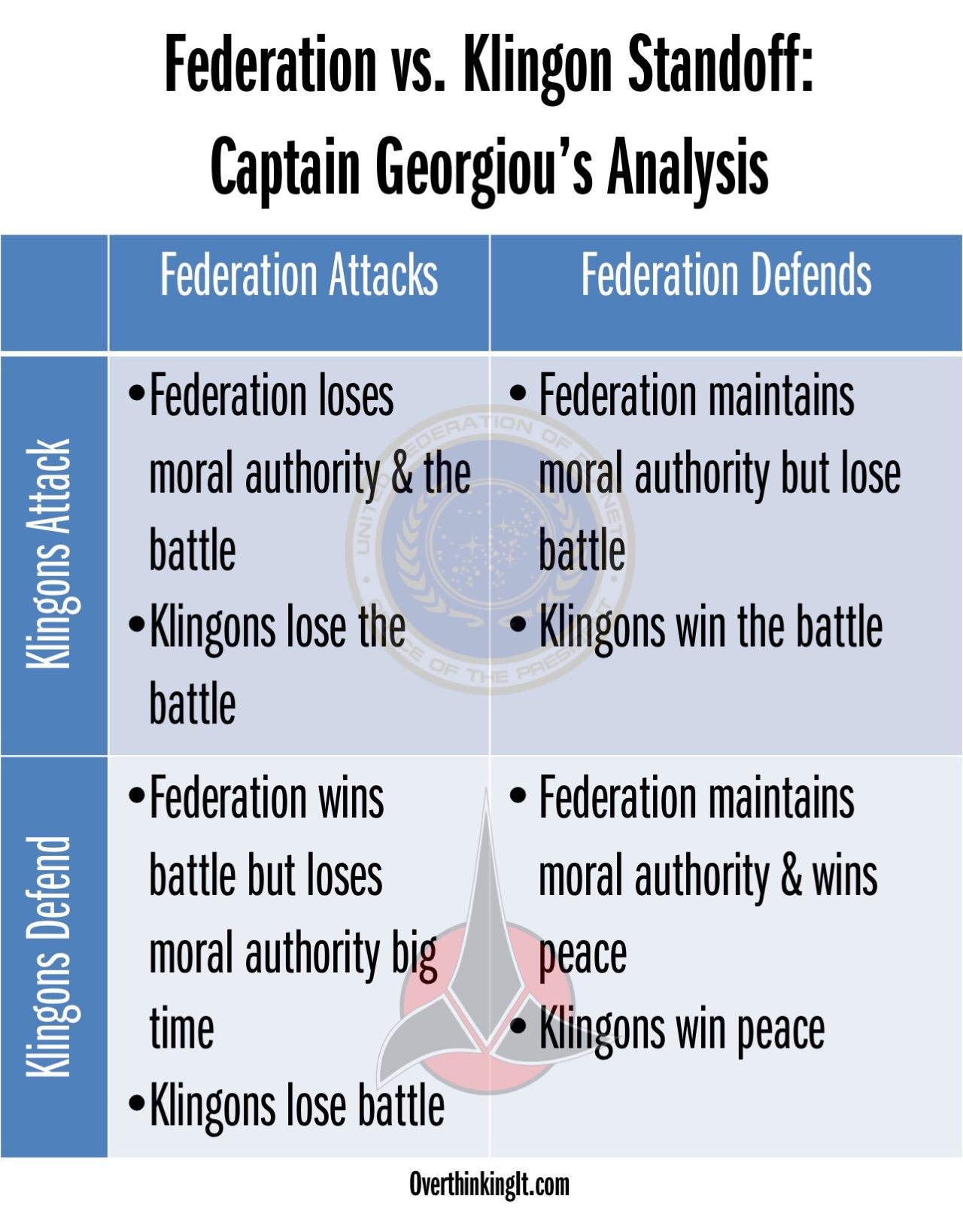
If the Federation maintains a defensive posture, the worst that happens is everybody on the Shenzhou dies while maintaining the Federation’s ability to negotiate with moral authority. In the best case scenario, nobody dies and everybody gets peace.
If the Federation attacks first, they may still lose the battle, but more importantly, they lose their moral authority, regardless of the Klingon’s intentions.
Defense: no brainer, right?
“The Klingon threat is always imminent, and inevitable.”
Burnham, when the walls fell.
Commander Burnham sees things differently. Based on her knowledge of the Vulcan’s past engagement with the Klingons, she assumes that the Klingons will attack unless its enemy has established a credible capacity for violence. The Federation’s moral authority is irrelevant to the Klingons, and Burnham is banking on the fact that other civilizations will take that into consideration.
Furthermore, as we see from the Klingon point-of-view sequences, T’Kuvma’s faction sees no honor at all in a peaceful co-existence with the Federation. To them, it’s either battle or capitulation, with no in-between.
Offense: the only logical conclusion, right?
Not really. Even though Burnham’s analysis of the Klingon side ultimately proved correct, the potential downside that Georgiou was hedging against was so potentially catastrophic that it’s hard to fault her for reaching that conclusion.
“Shoot first, ask questions later” is really not the Vulcan advice I was expecting.
And as Sarek warned, just because aggression worked for the Vulcans in the past wouldn’t guarantee it’d be appropriate for this scenario. The Vulcans apparently didn’t have to worry about sullying their reputation: the Sarek/Burnham FaceTime call suggests that it wasn’t common knowledge that the Vulcans acted so aggressively in its encounters with the Klingons. It was 240 years ago, after all. The same couldn’t be said if Federation starships acted the same way in an era where information flowed more freely throughout the stars.
And again, that was 240 years ago! A lot can happen over the course of 240 years. Imagine if a US Navy Commander made decisions about engaging the North Koreans in 2017 based on the Choson Dynasty’s military strategy as of 1777. That’d be highly illogical.
Which, the show suggests, is precisely the point. Burnham, scarred by her childhood trauma, is incapable of making a sober rational deduction when it comes to the Klingons. She’s beyond game theory, to say nothing of Vulcan logic.

