Enjoy this guest post from Dr. Daniel Alt!
Cartoon Physics, while not possessed of quite as extensive a pedigree as the more traditional variety, has nonetheless begun to receive the type of serious analysis previously reserved for the reality-based community. While the seminal work remains “O’Donnel’s Laws of Cartoon Motion” (O’Donnel, Mark, IEEE Institute, V.18 #7 p.12, 1994), the primary focus of these laws is classical cartoon mechanics.
While we are still awaiting our cartoon James Clerk Maxwell to synthesize an overarching theory of cartoon electrodynamics (which will almost certainly involve oversized Tesla coils and Jacob’s Ladders), in the present document we will attempt to formulate an approach to the equivalent to Einstein’s theory of relativity.
A key concept in cartoon physics is that of “Hammerspace.” While the term most likely originates with the fan community for the Japanese animated series, Ranma ½, observations of the phenomena date from far earlier. Hammerspace is the extradimensional space where cartoon characters, who traditionally lack pockets, store items too large for them to have been concealed about their person. When a tiny mouse pulls an enormous mallet from behind its back, that mallet was stored in Hammerspace.

Rigorous study of Hammerspace is quite difficult, as the observational data is very inconsistent (although it is clear that classical cartoon mechanics, being primarily concerned with the mechanics of falling bodies (particularly anvils) is not the appropriate tool for the analysis of Hammerspace). Sometimes it appears that a given instance of Hammerspace has virtually infinite capacity. For instance, in “I Am The Very Model of a Cartoon Individual,” Y. Warner produces a pie, a giant fish, exploding flowers, office desks, lava lights, Bert (who is a cannibal), and a giant book, which itself contains a secondary Hammerspace containing an anvil.
On the other hand, while there is clearly a Hammerspace storage pocket in Marge Simpson’s hair, she rarely produces more than one item at a time, suggesting that its extent is far more limited.
The key observation can be found by analogy to traditional relativity as postulated by Einstein and others. One of the central features of relativity is the constancy of the speed of light, c, in all reference frames. A consequence of this feature is that the term “simultaneous” is only meaningful for events which do not occur at any physical remove from one another, and that the perception of time differs between two observers moving at different velocities. To illustrate:
Imagine a coyote (Carnivorous Slobbius) has lit the fuses of two ACME® brand firecrackers on the corner of 1st Street. From the perspective of an observer on that corner, they explode ten seconds apart. Meanwhile, a Road Runner (Velocitus Incalculus) is running away from the corner at nearly the speed of light. From the perspective of the bird, the flash from the second one is much later than ten seconds from the flash of the first one, because he is almost, but not quite, outrunning the light. So from the bird’s point of view, time is running slower in the Coyote’s frame.
Meanwhile, from the perspective of the coyote observing the action from the precarious edge of a cliff at rest with respect to the intersection, the flashes do appear to be ten seconds apart. However, if the bird were holding a mirror (why not?) those reflected flashes would arrive more than ten seconds apart from each other, because it takes longer for the second flash to catch up with the Roadrunner than the first one. So from the coyote’s frame, time in the bird’s frame appears to be running slower, because the reflections are more than ten seconds apart.
What all this means is that there is no such thing as “absolute space” or “absolute time.”
Fortunately for sophomore physics students everywhere, it is possible to define a quantity which IS the same in all reference frames, but it involves combining both space AND time into one invariant called an “interval.” (Landau & Lifshitz, The Classical Theory of Fields, Pergamon Press 1951) Within one reference frame, say you have two points in space a distance L apart (in that frame) and an event that occurs at time t1 at the first point, and is observed at time t2 at the second point. The interval between those two points is defined to be:
![]()
If you then calculate this same quantity in a different reference frame, where the perceived times of the two events are t’1 and t’2, and the perceived separation between the points is L’, you’ll find that the total quantity is the same:
![]()
Sharp-eyed readers may notice that this formula is similar to the formula for finding the distance between two points on a plane:
![]()
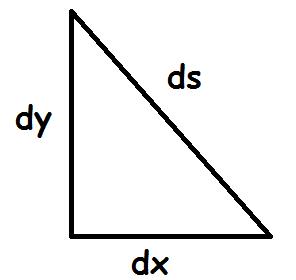
All cartoon physics illustrations are required to use Comic Sans. In reality-based physics, this is frowned upon, unless you are announcing the discovery of the Higgs Boson. (Cian O’Luanaigh, CERN, 2014)
To find the distance between two points, you square the x and y distances, add them, and take the square root. However, to find the interval between two points in spacetime you start with the square of the physical separation, then subtract the distance light would travel in the time separation.
So while there is no such thing as “absolute space,” you can nonetheless find something which is consistent and (somewhat) easy to understand by uniting space and time into one quantity.
One other important thing to mention about relativistic intervals: remembering that an interval is the separation between two events, one question that you can ask is, “Is there a reference frame where these two events appear to be happening at the same time?
If our roadrunner sets out from 1st Street at just under the speed of light, and a tiny instant later we set off the dynamite there, it’s going to take a little while for the light to catch up with it. (Him? Her? I actually have no idea which, if any, gender the Roadrunner chooses to identify with.) If we then set off a second stick of dynamite, just before the roadrunner reaches 2nd Street, and just as the light from 1st Street catches up with it, then the bird will see both flashes at once, and perceive the two events to be simultaneous. Whereas from our point of view, we set off the dynamite at a separation in time.
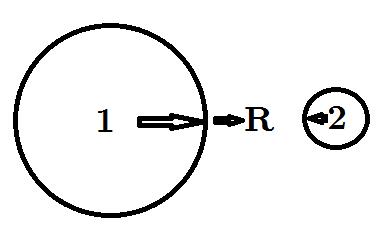
The Roadrunner will encounter both of these explosions at once, even though we perceive that 1 happened first.
If it is possible for a reference frame to exist where the two events are simultaneous, then the interval between them is considered to be “spacelike.” What about the opposite?
Say that we set off two sticks of dynamite at exactly the same place, but ten seconds apart. Is there any speed or direction at which the roadrunner can travel to see both explosions at the same time? No! The expanding spheres of light from the two events intersect nowhere, so the two events cannot be seen to be simultaneous, even if the roadrunner runs fast enough that the road does that thing where it leaps up off the ground like a flipped bed sheet.
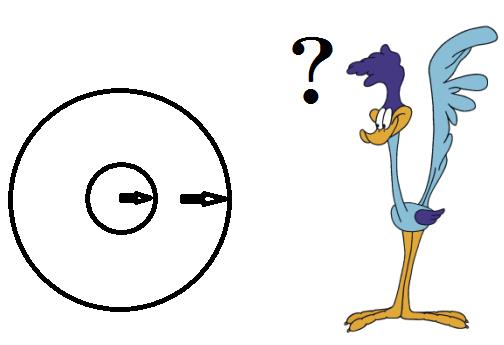
There is nowhere that the two circles intersect, regardless of how fast or where the roadrunner runs.
If there is no possible reference frame in which two events are simultaneous, the interval between them is referred to as “timelike.”
Positive values of ds2 are spacelike, and negative values are timelike. So there’s a balance – in any given reference frame, the farther apart two events are physically, the closer together they must be in time to be spacelike. Once the separation in that frame is greater than the distance time can travel in the separation in time, then the interval is timelike.
So how do we now apply this to the topic of Hammerspace? It is clear that the reason that all previous attempts to rigorously treat Hammerspace have failed is that relativity has not been properly taken into account. (Note: There have been no prior attempts to rigorously treat Hammerspace.) In other words, there is no “absolute Hammerspace.” But we can find something meaningful by uniting it with the obvious counterpart:
Hammertime.
Hammertime (first postulated by S. Burrell, 1990) is a form of time with a few unique properties. First, unlike conventional time, which proceeds always in a single direction (Eddington, The Nature of the Physical World, MacMillan, 1928), Hammertime can be completely stopped.
This already has drastic implications for Hammerspace; while conventional space is paired with a time which constantly moves forwards, Hammerspace can be defined in terms of a time separation which can remain zero in all cases. What does this mean? All intervals can now be made spacelike!
Consider our previous timelike case – two sticks of dynamite set off ten seconds apart. It doesn’t matter how fast the roadrunner runs – if they are on the expanding light sphere of the first stick, the roadrunner cannot also simultaneously be on the sphere of the second one. However, with the addition of Hammertime to our understanding, there are any number of ways to address this.
For example, consider this sequence of events:
- Light fuse on dynamite at 1st Street.
- Place dynamite in ACME® Hammerspace safe, and close the door just as it explodes.
- Move safe to 2nd Street.
- At your leisure, set off a second stick of dynamite at 1st Street. With Hammertime stopped within the safe, you can wait as long as you want because…
- When the light from the second stick of dynamite reaches 2nd Street, you can open the safe, and you will perceive both events as simultaneous. Ergo – spacelike, regardless of separation in time.
Now the various properties of standard relativity arise because of the experimentally confirmed fact that nothing can travel faster than the speed of light, and the speed of light in vacuum is constant in all frames. What underlying principle can we use to frame our Grand Hammerspacetime theory?
I propose Burrell’s First Law of Hammerspacetime Special Relativity:
“There exists a thing, ‘this,’ such that ‘this’ cannot be touched by ‘you’ in any reference frame.”
The untouchability of this by you is clearly only possible because of the stoppage of Hammertime – otherwise, there would always be some reference frame in which you could touch this. Since there is not, then Hammertime must be stopped, and the spacelike nature of all intervals in Hammerspace is confirmed. QED.
Daniel Alt is a professional roller derby referee who builds particle accelerators in his spare time. Or possibly the other way around. Yeah, it’s probably the other way around.

Add a Comment