Like all good geeks, I have a soft spot for Superman II. Today I want to overthink one scene in particular… and surprisingly, it does not feature the line “Kneel before Zod.”
Early in the film, Lois and Clark are on assignment at Niagara Falls. A little kid is playing on an observation platform, and his grip suddenly slips. He falls off the Falls… and falls… and falls…
http://www.youtube.com/watch?v=RSc-V3aq85Q
So here’s my question: how far would a child really fall in 28.4 seconds?
Well, figuring out how far something falls in a vacuum is pretty easy:
Figure 1
Here on Earth, “acceleration due to gravity” is about 9.8 m/s2. So let’s plug in our numbers.
That’s 12,966 feet, or 2.46 miles.
So according to Superman II, Niagara Falls is 2.46 miles tall (plus like 20 feet, since Superman catches the kid a little above the water).
Hahaha! Let’s all enjoy a good laugh at that! That is WAAAY taller than any real waterfall!
Unfortunately, we don’t live in a vacuum. Which makes that number completely worthless. To find the REAL height of Super Niagara, we have to account for air resistance.
And this, I’m afraid, is where the pain begins. As far as I can tell, there’s no formula on the internet for “distance a little boy falls in a given length of time,” so I derived the equation myself. And by “derived,” I mean “emailed a couple of brilliant friends and had them figure this out for me.” I myself spent most of AP Math playing Drug Wars on my TI-82 (which was totally worth it). So I’d like to thank David Shechner and Emily Neubauer for dropping some science on me.
Warning: the math that follows will seem a lot more interesting if you listen to this while you read:
[audio:http://www.overthinkingit.com/wp-content/uploads/2008/09/superman.mp3]Okay, let’s jam.
If you’re traveling at a constant velocity, then the basic equation for distance is:
Figure 2
For instance: if you drive 60 mph for 2 hours, you travel 120 miles.
But that only works if velocity is constant. If you’re gradually putting the pedal to the metal as you listen to Appetite for Destruction, Figure 2 doesn’t apply.
However, there is another way to express Figure 2, which allows for velocity to be an equation. It’s called an Integral:
Figure 3
A brief review of what Integrals are. Take the example of the accelerating car again. 
Imagine you record the car’s speed every minute, and then later use those measurements to estimate your total distance. You’d maybe be in the ballpark.
Now imagine recording your speed every second. Obviously, you’d get a lot closer to the real distance that way.
An Integral allows you to subdivide your car trip into an infinite number of pieces and add up the distance traveled during each of those slivers. That’s Calculus, and it’s why I majored in Humanities and fulfilled my science requirement by taking “Science Fiction/Science Fact.”
So what we need to get started is an equation that tells us how fast the kid is falling at any point in time. And luckily enough, Wikipedia has it for us here, about halfway down the page:
Figure 4
Don’t panic. Deep breaths. We will get through this.
First, what the hell do all these letters mean:
m = mass of the falling object
I’m going to guess that the kid weighs about 70 pounds, which is about 32 kg in science talk.
g = acceleration of gravity
This is still 9.8 m/s2.
p = air density
Air density varies depending on the temperature. Assuming it’s a pleasant 68 degrees (20 Celsius in science talk), than P is about 1.2 kg/m3.
A = surface area of falling object
What, exactly, is the surface area of a kid tumbling through the air? Well, let’s assume he’s four feet tall and a foot wide, and he’s sort of spread out as he falls… I’m very roughly estimating .4 meters. You wanna argue, that’s what the comments are for.
Cd = drag coefficient
This is a measurement of how aerodynamic something is, and there’s no way to calculate it without building a wind tunnel or spending four sexless years at CalTech. This page says the drag coefficient of a skydiver is about 1. Let’s go with that, because it’s my favorite number to do math with.
“Tanh,” by the way, is short for “hyperbolic tangent.” I don’t really know what it is, but I do know there’s a button on my calculator that says “tanh,” so I can solve it.
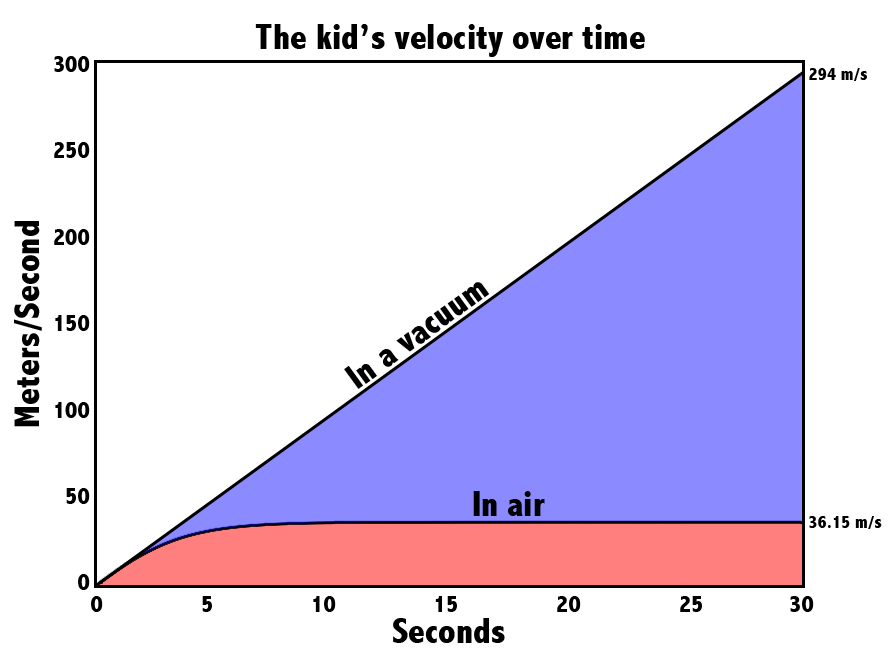
Let’s test out the velocity equation in Figure 4 with the numbers we just picked out. The results are the red curve on this pretty graph (yes, I used Superman colors on purpose).
Figure 5
The straight diagonal line is what happens to the kid’s speed when he falls in a vacuum. He just keeps accelerating, which sucks for him, but luckily the vacuum has already killed him.
In the air, it’s a different story. After about ten seconds, he reaches terminal velocity. That’s when the force of gravity is equal to the force it takes to push all that air out of the way. He’s still falling – he’s just not speeding up anymore. It seems like for this kid, terminal velocity is around 36.15 m/s, aka 81 mph.
But let’s keep our eyes on the prize – we’re trying to find the DISTANCE the kid falls in 28.4 seconds, not the speed he’s traveling at the end of it. So let’s plug Figure 4 (velocity equation) into Figure 3 (Integral for distance).
Figure 6
That’s technically the equation we’re looking for. But we’re not quite ready to plug our numbers in yet. Before our Integral can be solved, it has to be simplified (“simplified” is relative here).
See that first square root in the Integral, before “tanh”? Well, that’s a constant, actually. None of those variables change (it’s not like the kid is getting fatter while he falls). And a constant can be moved outside the Integral (trust me on that). So we get the tidier:
Figure 7
And when I consult my handy Integral Chart, which I keep by my bedside at all times in case of emergency, I find this:
Figure 8
More fun letters! “Ln” means “natural logarithm.” That’s another button on your calculator you don’t have to know the meaning of to solve this. Ditto “cosh” (“hyperbolic cosine”). Those vertical lines at the end mean “absolute value.” As in, “Hey, if the number inside these lines turns out to be negative, just pretend it’s positive, mmkay?”
The “whatever” is a constant that multiplies the variable inside the Integral. And if you take a peek back at Figure 7, you’ll see that in this case…
Figure 9
Alrighty then. We’re ready to un-Integral our Integral, by applying Figure 8 to Figure 7. Brace yourself – it ain’t pretty:
Figure 10
Then again, maybe it is pretty. Because once you simply those first couple of terms, you have what we’ve been dreaming of. Ladies and gentlemen, I present to you, for the first time on the internet…
Figure 11
Now, all we have to do is add the numbers and crunch ’em.
Figure 12
Not nearly as large as the first number we came up with waaaaaay back at the top of this page. But pretty darn tall. According to (man, I can’t believe this exists) the World Waterfall Database, the highest single drop from a real waterfall is 2,648 feet, off Angel Falls in Venezuela.
I wanted to illustrate what you’d have to put on top of Angel Falls to equal the height of Superman II Niagara. According to IMDB, Godzilla is exactly 400 feet tall. So there you have it: if Godzilla was standing on top of Angel Falls, and a little boy was standing on top of Godzilla, and the little boy fell, he’d fall for 28.4 seconds before he splatted in the Veneuzelan jungle.
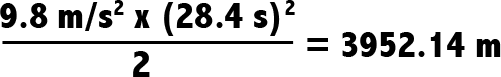
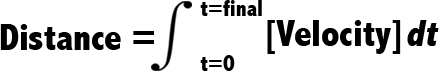
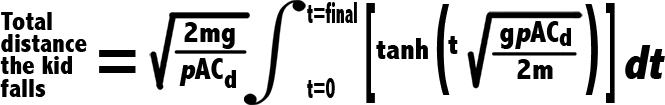
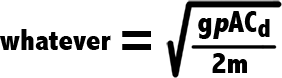
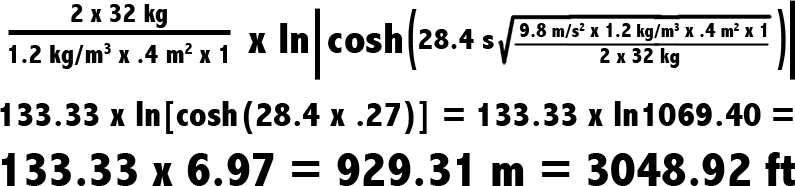
Wow. I kneel before your maths.
I love the kneel before newton line. I also applaud you for not shying away from air resistance. When i started this article i thought to myself if they just stuck with in a vacuum i’ll be annoyed. but you guys pulled it out congrats
This math isn’t all THAT complicated.
Besides, you’ve assumed laminar air flow.
C’mon Dan – I was counting on you heavyweights to get into long complex mathematical arguments in the comments.
Well, I feel like sludge right now. I’m… Uh… Puppies?
so, here’s an easy question that i’m asking out of laziness: how long WOULD it take you to fall down the Niagara Falls?
Damn! That’s some good over-thinking!
Now, if we take the given equation and switch it around so we get t=(blah blah) you get
[five minutes and some scribbling later]
t = acosh(e^(DpAC/2m)) / sqrt(gpAC/2m)
where
t = time
acosh = reverse-cosh
e^ = e to the power of… , where ‘e’ is a constant, kinda like pi. e^ is the reverse of ln
D = distance
p = air density
A = surface area
C = drag coefficient
m = mass
sqrt() = square-root
g = gravitational acceleration
Plugging in the numbers above, plus 51m for the height of Niagara (taken from the afore-mentioned word water fall database) and we get
[five minutes and some stabbing at a calculator later]
5.27 seconds
I’ll just take a moment to promote one of my favorite old Web sites, Insultingly Stupid Movie Physics —
http://www.intuitor.com/moviephysics/
Sorry, you’ve done everything right as far as I can tell, no complex argument here.
But here’s another good physics link:
http://funnies.paco.to/cartoon.html
The real mystery here is; why does the chick start shouting ‘Help! Somebody help!’? Does she actually expect somebody to help? And do what exactly? Quickly attach their bungee harness and dive in? Unless she KNOWS supes is nearby, and uses the word ‘somebody’ in an implicit sense. Hmmm… The plot thickens…
So what you’re really saying is that Superman threw the boy up in the air 400 feet and then he fell over the waterfall, only to have Supes grab him again, in some twisted game of self-fetch. That’s disgusting.
Now that you’ve bought this error to light, I think it’s about time that they remade Superman II with a better respect for physics. For a start, they can get rid of that flying chappie.
so how long did it take you to write the article
I think most of this is still rather pointless , surely the boy would still die from his impact of what is effectively landing on supermans arms at near terminal velocity ?
Someone mentioned laminar airflow. You also might want to add the possibility of an updraft. Here’s some fun over-thinking: How much of an updraft is required to compensate for the actual height of Niagara Falls? My simplistic solution would be to subtract that value from the 36.15m/s velocity reached in the “in air” solution. Assuming the kid was falling at the maximum velocity the whole time (which is wrong only for the first ~5 seconds of the fall), the velocity to fall 51m in 28.4 seconds is ~1.8m/s. So there could have been a 34.35m/s (77mph; a hurricane on the Beaufort scale) updraft. NOTE: I did this math in less than 10 minutes, so corrections are welcome and expected.
Here’s another thought that may make this entire calculation inaccurate. Time shown in a movie is not precisely linear. Events that are shown in one cut can overlap with events that are shown when the camera cuts to another POV.
For instance, the mother runs to the rail and yells for help. The camera cuts to Clark running past the ice cream stand. Clark is running at the same time the mom is yelling, but they happen in sequence on film. So that four seconds of film time actually covers the same two seconds. This occurs with much of the boy’s fall, as well. So he’s really not falling for 28.4 seconds. However, without the uncut footage, or without tossing a 70-lb boy off Niagara Falls, it’s nearly impossible to calculate the actual falling time.
At first, I definitely thought Lois crying for help was silly. But you know what? I’d do the same thing. I mean, it’s not like you’d see the kid falling and think, “That kid’s a goner. No point in bothering anyone about it.”
Belinkie:
Have you tried re-editing the clip taking cuts into account? How much time do we actually see him falling?
Maybe that’s where all of our answers lie.
This scene never quite sat right with me. The kid does appear to fall for an unusually long period of time.
Math aside, I’ve stood on the exact spot at Niagra where this was shot. The place the kid falls over the edge of the falls has decent size ledge no more than 10 ft below. In all likeliness, he would have suffered a broken bone or 2. Worse case a broken neck… 9ft falls have been known to be fatal.
This reminds me of the old engineering joke. Three students are given a barometer and asked to calculate the height of a building. One from School 1 throws the tool from top and uses distance theory, one from School 2 measures atmostpheric pressure at the top and bottom and uses the difference to calculate the height, and the third from School 3 – the school being insulted = walks up to the janitor and says “I’ll give you this nifty barometer if you tell me how high your building is.”
Like all graduates of Case Tech in Cleveland, I would have just asked a friendly skydiver how far he would fall in 26.3 seconds.
So did Supes break the sound barrier when he went after the kid and, if so, are all those tourists deaf as a result? Would said tourists be allowed to file a class-action lawsuit against Superman for the pain and suffering he inflicted in his sudden rush to save one little boy? Do the needs of the one really outweigh the needs of the many? Huh, huh, does it, does it? Ha!
This is awesome! The article is great, well thought out and funny, and the comments are as well! (Especially Tony’s comment about “the flying chappie”).
Good job!
Thanks for that article! But I think if you do scientific maths, you should always use the metrical system and not that awful imperial stuff like feet etc. Yuck!
There’s this concept in filmmaking called “parallel action”, where two things which are happening simultaneously are shown one after the other. I am not going to dissect this clip shot-by-shot, but I bet you could cut that 28 seconds in half if you assume half the action shown happens simultaneously.
BUT Supes has to be careful to slowly decelerate while catching the falling boy- he might break every bone in his body anyway!
See the thing is Superman does everything from the moment he sees the child fall in a split second, I could say a millionth of a second but then I have no idea what that means…
So everything happened in normal “fast” time we just saw it in “real” time…because how boring would it be to see nothing but a Super blur?
The real question is where did the kryptonians learn english? Especially that “KNEEL BEFORE ZOD!!!” We know Superman learned it here on earth.
I’ve watched this clip a BUNCH, and I don’t think there’s any parallel action going on here. There’s nothing about the way this was shot or edited that implies that time is unfolding any way but normally. If you’re feeling very generous towards the director, you can give him the benefit of the doubt and shave some seconds off. But clearly, the kid would have already hit the water by the time Lois got Clark’s attention.
Actually, I give the director some props for pulling the sequence off as well as he did.
Wow. Funny math dudes. Who’d a thunk it?
Terrific entry. It has so many things I love: Superman, skeptical inquiry, the ruination of everyone’s credulity, etc.
Now how about figuring out exactly how fast one must fly in order to go back in time, a la the first Superman movie?
The going-back in time thing is easy (well, if you know your special relativity)
The faster you go, the slower time appears to pass in your surroundings (“surroundings” meaning anything travelling slower than you). When you hit the speed of light, time appears to stop in things that are stationary relative to you.
Now, if you travel at a speed greater than the speed of light the equations break. You start dealing with square-roots of negative numbers, which results in imaginary time, which I suppose is kinda like movie time…
Problem is, you can only travel at the speed of light if you have zero mass, and you can’t go faster than that at all. Well, maybe if you had negative mass, or imaginary mass…
Other problem is this only works if you go in a straight line.
this is a fantastic article. thank you for helping to bring math into the realm of pop culture.
Who gives a shit? Superman isn’t real. Come on, Superman is like the ulitmate Superhero, but he isn’t really you can make up anything in a Superman movie and it will work.
Forget all that complex math, where’d you get the nifty time in the Supe viddy?
er uh I mean timer.
I can’t believe no one’s commented yet on the brilliant “of course he’s Jewish” throwaway line…
Hey! No fair!! You start with the solution (almost) when you give the velocity in terms of tanh.
Now, if’n we’re to listen to good ol’ Newton, we’d write:
Force = (mass) (acceleration) or F = ma
and that gives
(Gravitational Force)-(Drag Force) = mdv/dt
and the Maximum Velocity (actually it’s the “speed”) is when
(Gravitational Force) = (Drag Force)
’cause that’s when dv/dt = 0 and the kid ain’t changing his speed.
So we got
mg (that’s Gravitationl Force) = k v^2 (that’s Drag Force)
assuming (Drag Force) is proportonal to velocity^2.
(Did I mention that it’s really the “speed”, not the “velocity”?)
If’n we didn’t take this short cut, we’d have to solve a differential equation, eh?
m dv/dt = m g – k v^2
which’d give us a tanh function
… and we don’t wanna do that!
So then we got: m g – k v^2 = 0
so: Maximum Velocity = SQRT[mg/k ]
Now Drag Force is like so:
Drag Force = k v^2 = (1/2) C p A v^2
where C depends upon the geometry of the falling kid
and p is the density of air (kg/m^3)
and A is the cross-sectional area of the falling kid (and NOT the surface area )
… and it’s in square metres.
So we now got:
k = (1/2) C p A
so
Max. Velocity=SQRT[mg/k ]=SQRT[2mg/C p A]
which turns out to be 36.15 m/s
– using Matthew’s numbers
– jest like on Matthew’s Neato Chart.
If he fell at that Maximum speed for 28.4 seconds, he’d have fallen over 1000 metres.
Note (from Matthew’s Neato Chart) how quickly the Maximum Velocity is reached.
Note, too, that if the kid fell over while driving a Hummer then the drag coefficient, C, would be 26.5
(instead of C = 1) and he’d fall only about 200 metres … but the Hummer would be toast.
P.S.
I jest changed the Drag Coefficient.
If’n I also change the cross-sectional area and the weight, the kid+Hummer would fall about 500 metres
… but the Hummer would STILL be toast :^)
Laminar airflow and updraft have been mentioned, but there’s also a straight-up error in your calculations: you use a constant for air density, in other words assuming dry air, when the air around Niagara Falls has practically 100% humidity.
The kid deserves a superpunch for his stupidity. Superman took his time on that one deliberately, methinks.
After the kid drowned, Supes had doubts about his decision, gave out a wistful shriek, and flew back in time in spite of his father’s warning a second time. Who knows how many times Superman has reversed the events of the world if there is such a quick-fix to be had?
Here is one problem… film shows tow or more different places during this 28 second… For example: 1. waterfall, 2. the place where superman is… 3. somewhat ship and so on… Film director may considered that while the woman shouts for help then superman is shown hearing this cry this can’t be different time and this happens at the same time…